Concept of Real Numbers: In very general terms real numbers are considered to be the perfect combination of the rational as well as irrational numbers in the world of the number system. In general, different kinds of arithmetic operations can be performed on all these kinds of numbers and they can be represented on the number line as well. At the same time, imaginary numbers are considered to be unreal numbers that cannot be expressed on the number line and are usually used in terms of representing or describing complex numbers. There are several kinds of concepts associated with the real number system and some of those are explained as follows:

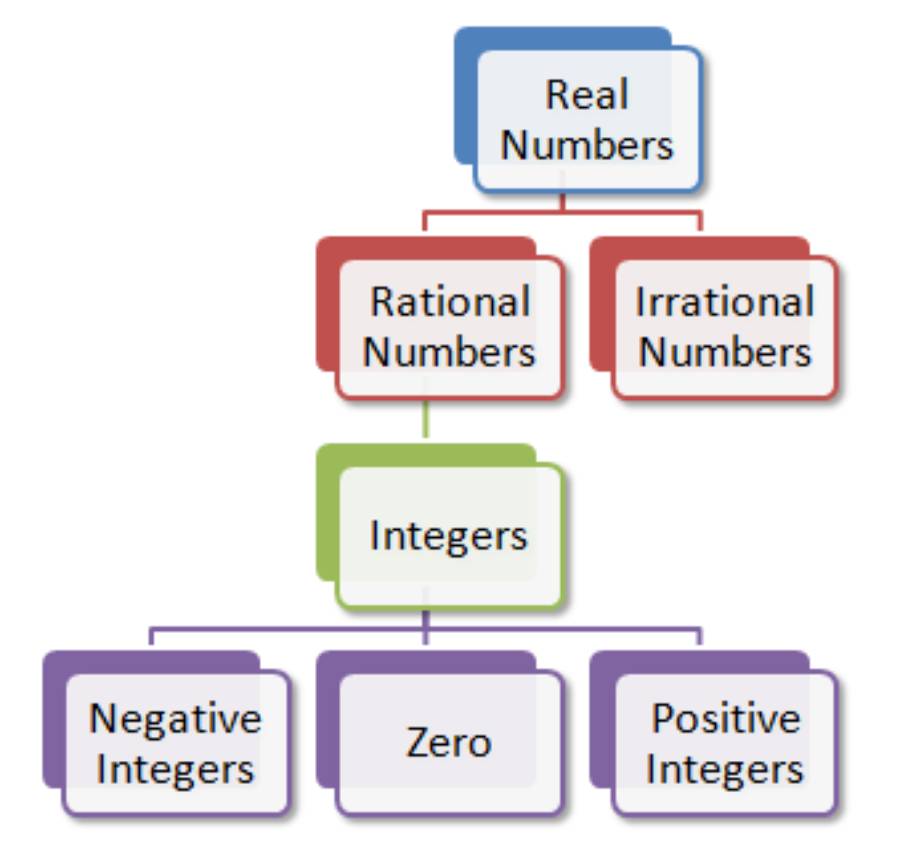
As a very basic matter of fact, real numbers are considered to be the union of both rational and irrational numbers and they can be both positive as well as negative. All the natural numbers, fractions and decimals will be coming into this particular category.

The set of real numbers will be consisting of different kinds of categories and all the components of the real numbers are explained as:

• Natural numbers will be containing all the counting numbers which will be beginning from one for example one, two, three, four and so on.
• Whole numbers will be the collection of zero as well as natural numbers and these will be the natural numbers +0 for example zero, one, two, three and so on
• Integers will be the collective result of whole numbers and negative of all the natural numbers for example 3, -2, zero, one, -4 and so on
• Rational numbers are the numbers that can be perfectly written in the format of P/Q for example 5/4, 12/16 and so on
• Numbers are the ones that cannot be written in the form of P/Q for example root two, root three and so on

The people need to be clear about the chart of the real numbers as well so that overall goals are very easily achieved and identification of such numbers and components becomes very easy.

The topmost properties of the real numbers are explained as follows:

1. If there will be two real numbers then in the cases of addition M plus N will equal to N plus M and the order will never matter. This particular property will also be applicable in the cases of multiplication and will be known as the commutative property of numbers.
2. Real numbers are also very much capable of justification of the associative property both in the cases of addition as well as multiplication.
3. The distributive property will also be perfectly represented in the cases of real numbers so that there is no issue at the later stage.
4. Identity property will also be there in the case of real numbers which can be explained in the form of addition M +0 is equal to M so, zero here will be the additive identity and on the other hand in the case of multiplication M into one is equal to 1 into M and the result will always be N which will mean that one is the multiplicative identity in this particular area.

Concept of Real Numbers : This particular concept is usually introduced in the lower classes of mathematics and further people need to be very much clear about the representation of the real numbers on the number line and performing different kinds of operations as well. Apart from this people also need to be clear about different kinds of laws associated with the exponents so that evaluation of the things can be done very perfectly and there will be no issue at any point of time. Hence, depending on platforms like Cuemath is the best way of ensuring that people will also be having a good command over Roman numerals so that they can avail several kinds of advantages in day-to-day life very easily by having a good command over this concept.